聚类热图
聚类热图(Cluster heatmap)常用于大数据表数据关系的可视化展示,以便快速阅读和发现规律。
默认情况:
- 少于2个样本时,不绘制热图;仅2个样本时,不对数据进行归一化
- 默认条件下,行列聚类,输出聚类后排序列表,限制绘图特征数目上限为 65536 个,聚类特征上限为14000个;
- 可根据参数自定义热图,默认不显示特征名称,若显示特征名称时,可选择对字符串(70个字符)进行截取;
- 某特征在所有样本中数值相等(方差等于0)时将自动删除,并提供warning文件;
- 存在相同特征时,将自动计算表达量之和且保留高表达特征,并提供warning文件;
- 分析前请检查数据是否完整,不允许有空值。
1.图形说明
示例图片为默认参数下的聚类热图。示例图片中,一个小方格代表一个基因,其颜色代表该基因表达量大小,红色表示高表达基因,蓝色表示低表达基因。图片上方树形图表示来自不同实验分组的不同样品的聚类分析结果,左侧树状图表示对来自不同样本的不同基因的聚类分析结果。
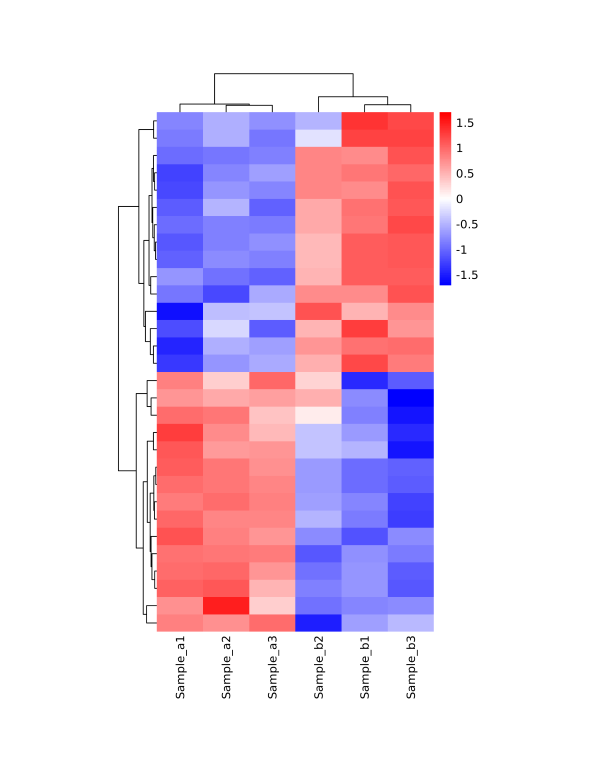
2.表格输出
若选择行/列聚类,将输出聚类后顺序文件,“heatmap.reorder_cluster_result.xls”。示例图片中,基因名顺序已为聚类分析后排序,并补充各样本表达量信息。

1.表达量矩阵文件(必选):
表达量矩阵文件为必填参数,第一列为基因/蛋白/代谢物名称,其余各列为各样品中相应表达量。输入文件格式支持xlsx、csv、txt和xls,文件名不允许有空格和特殊字符,外来数据请先调整数据格式。

2.样本分组信息文件(可选):
示例文件为样本分组信息,需包含列名 "Sample", "Group"。

3.注释信息文件(可选):
示例文件为表型数据。

主成分分析PCA
主成分分析(Principal Component Analysis,PCA),是对原有的复杂数据进行降维,保持数据集中对方差贡献最大的特征,去除噪音和冗余,从而有效地找出数据中最“主要”的元素和结构,主要影响因素区分各个样本,根据样本远近展示样本/分组间的相似性和差异性。
默认情况:
- 少于等于3个样本时,不进行主成分分析;
- 默认条件下,不对数据做任何处理,各平台数据过滤方式不同,请注意输入文件是否属于以下类型:芯片、转录组测序、微生物多样性OTU;
- 绘制置信椭圆,需添加样本分组信息文件,且组内生物学重复需为4个样本及以上。
- 分析前请检查表头是否完整。
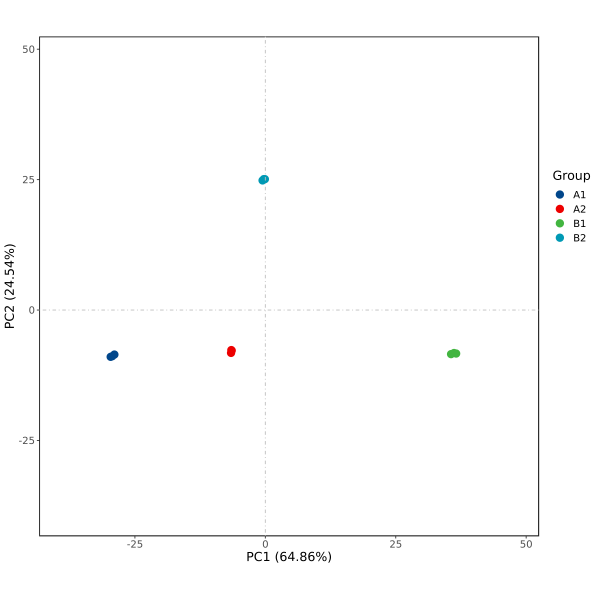
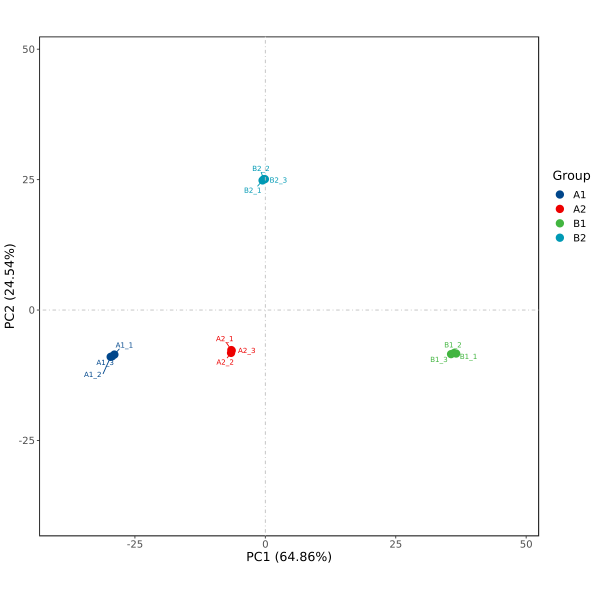
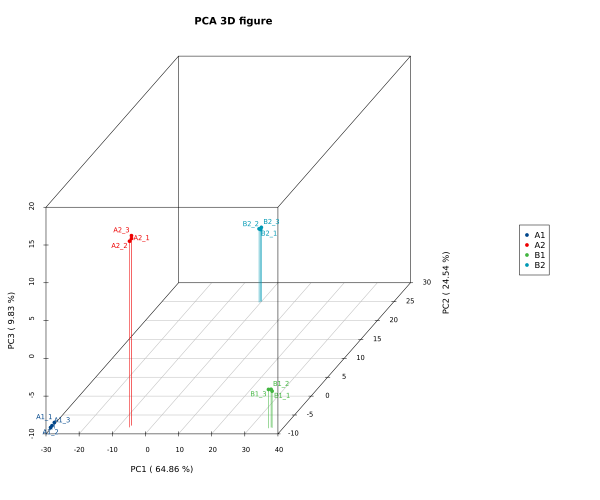
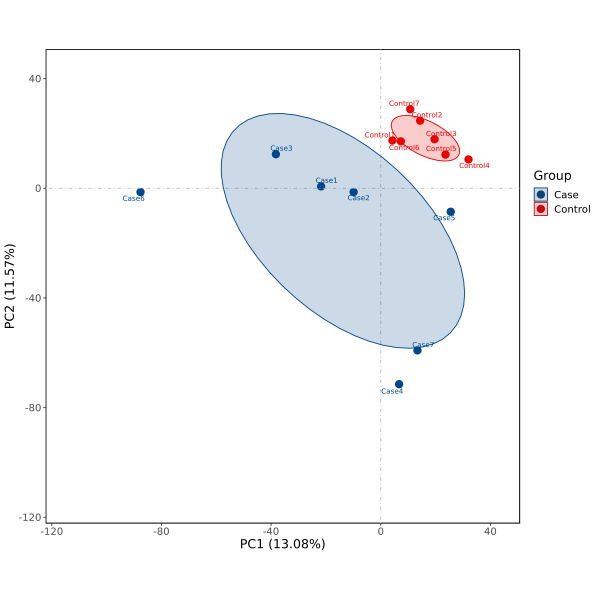
1.图形说明
结果生成pdf、png格式,PCA 2D图,使用主成分1(PC1:Principal component 1)和主成分2(PC2:Principal component 2)作为X轴和Y轴绘制散点图,分别提供无标签及添加标签形式。
PCA 3D图使用主成分1、主成分2和主成分3分别作为X轴、Y轴和Z轴绘制散点图。
PCA 2D图,添加置信椭圆。
1. 矩阵文件(必选)
矩阵文件为必填参数,第一列为探针/基因/OTU名称,其余各列为各样品中相应检测值。

2.样本分组信息文件(可选):
示例文件为样本分组信息,需包含列名 "Group"。

火山图
火山图(Volcano Plot)是一类用来展示组间差异数据的图像,可以方便直观的展示两组样本间差异表达基因/蛋白/代谢物的分布情况。
默认情况:
- 当输入标记名称列表文件时可展示相应名称,如genesymbol,限定标注15个以内名称;当大于15个名称时则以紫色点标注。
- 当输入文件中 log2FoldChange 为空值时,将自动以最小值进行替换,请谨慎修改文件数据。
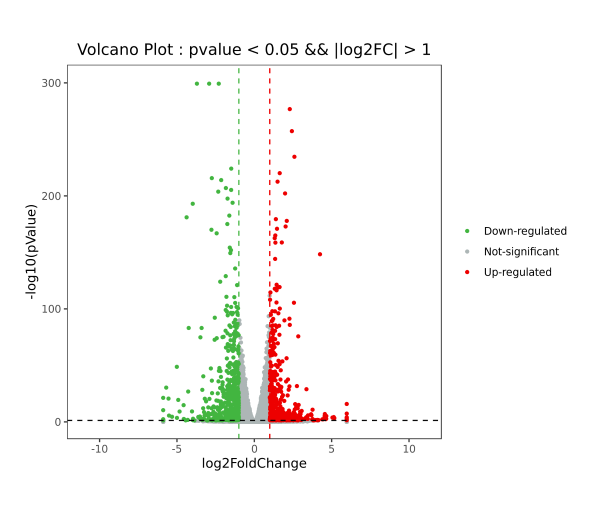
1.输出图片
示例图片中每一个点代表一个基因。横纵坐标分别表示实验组(Case)和对照组(Control)生物学重复差异倍数FC值的对数值。根据基因表达差异倍数FC值的筛选,红色表示显著上调基因,绿色表示显著下调基因,灰色表示差异不显著。
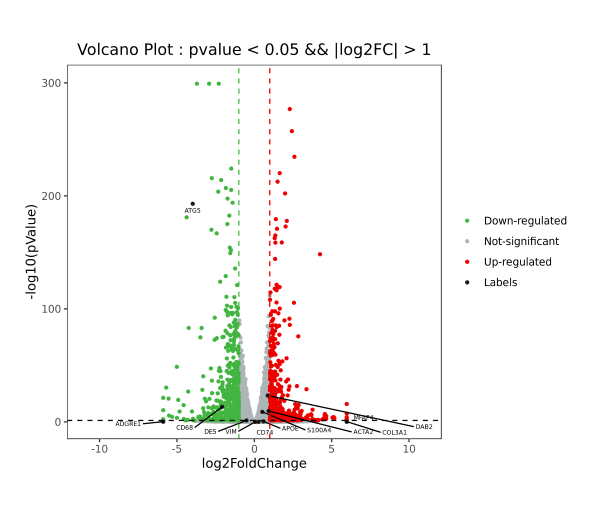
示例图片为标注名称,以黑色点展示。
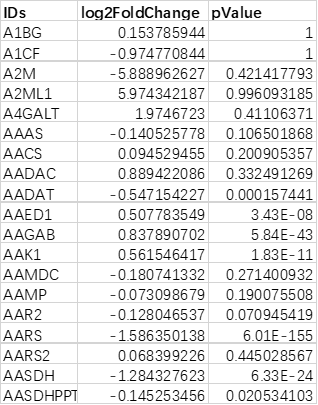
1. 差异表达未筛选文件(必选):
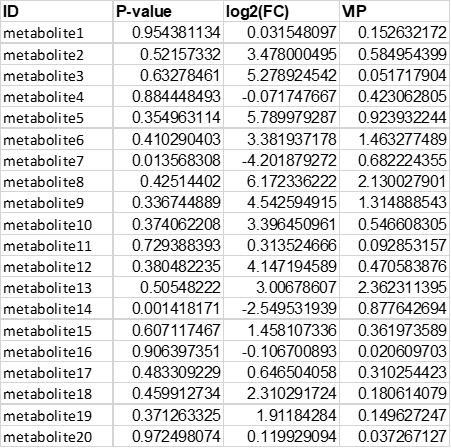
示例文件为基因表达量差异未筛选文件,第一列为基因/探针名称,第二列是 log2FoldChange ,第三列为 pValue ;代谢组数据第四列可为 VIP 。 输入文件格式支持xlsx、csv、txt和xls,文件名不允许有空格和特殊字符,外来数据请先调整数据格式。 [测序/芯片组数据整理格式]
[代谢/蛋白组数据整理格式]
2. 芯片组差异文件(对芯片数据绘图时必选):
示例文件为芯片差异结果列表,需包含列名 "ProbeID"。

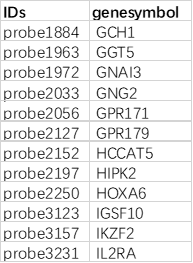
3. 标记名称列表文件(可选):
示例文件为标记名称列表,需包含列名 "IDs"。

示例标记名称列表文件
Venn图
Venn图,又称韦恩图或文氏图,是一种用于直观表示元素集合重叠的一种图形。Venn图在生物信息学领域常用于展示样品不同分组间共有和特有的基因、OTU和分类单元等。
注:
- 根据输入数据的不同,可以设置为单文件的venn分析作图(参考使用方法一)和多文件的venn分析作图(参考使用方法二)。
- venn图仅支持低于5个集合绘图,超过5个集合请使用upset绘图工具
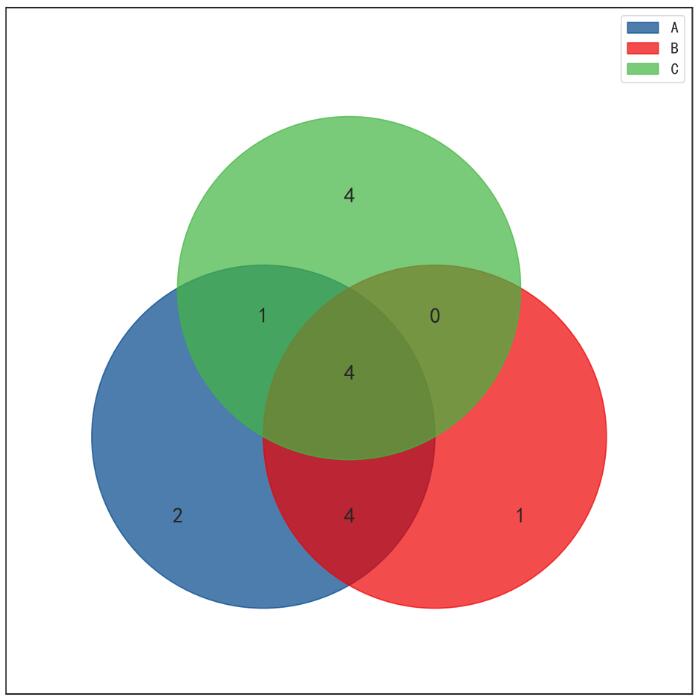
1. venn图
示例图中一个圈表示一个集合,其中的数字表示各区域交集元素数量。
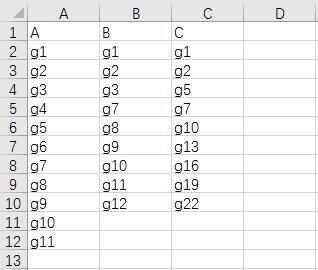
1. 方法一(单表格输入)
每列数据为一个数据集,包含不同数量的基因(如下示例可以通过Venn分析工具展示A,B,C这3个数据集之间的关系。)
2. 方法二(多表格输入)
(1)每个表格表示一个集合
(2)表格第一列信息作为该表格的元素的集合(如探针,转录本,基因名称)

3.保存结果类型:
默认保存venn交集结果信息,也可选“并集”或“每个区域均保存”,“每个区域均保存”即导出venn图上每个数字对应元素集合表格。
GO/KEGG气泡图
气泡图,用于展示富集分析结果中P值最小的前N个功能或者通路。其中Y轴对应功能或者通路,X轴表示特定通路中的差异基因和通路中所有基因的比值,气泡的大小表示该通路中差异基因的多少,气泡颜色由紫-蓝-绿-红变化,其富集 pValue 值越小,显著程度越大。 通过气泡图,可以生动地展示富集分析结果中的各个关键统计量,从而在一张图上呈现更多的信息。 富集结果的呈现也有利用条形图来展示的。
1. 气泡图
示例图中Y轴对应功能或者通路的名称;X轴对应特定通路中差异基因与该通路所包含的所有基因的比值,值越大,说明该通路的差异基因占比越高;气泡图上的点表示差异基因的多少,点越大,特定通路中的差异基因越多;
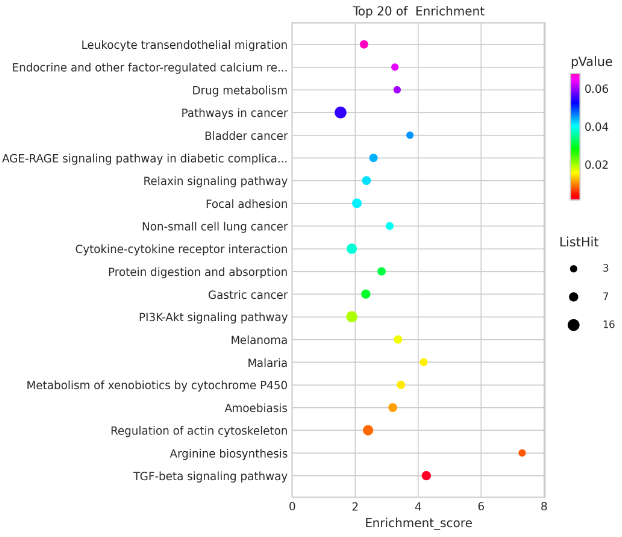
1. 输入数据:
输入表格需包含中"Term_description”、“ListHit”、“Enrichment_score”和“P_value”列。【文件格式支持:txt,csv,xlsx,xls】

注:推荐使用芯片报告中富集结果原文件,或对原文件中GO或KEGG条目进行删减(挑选)后的文件
GO富集条形图
Gene Ontology(GO) 数据库提供了专业的术语来定义基因产物的属性。它包含三大类:生物学过程(Biological Process, BP)表示一个分子活动事件的过程,包括细胞、组织、器官和物种的功能集合,往往也是和实验研究问题关联程度最高的一类;细胞组分( Cellular Component, CC)表示细胞或其所处的外界环境;分子功能(Molecular Function, MF)是描述在分子水平上基因产物的活性元件。
默认情况:
- 筛选三种分类中对应差异基因数目大于等于 3 的 GO 条目,按照每个条目对应的 -log10pValue 由大到小排序的各 N 条,可对富集结果进行筛选;
- 可选择对字符串(70个字符)进行截取。
1.图形输出
示例为OE常规转录组分析中GO富集条形图,筛选三种分类中对应差异基因数目大于等于 3 的 GO 条目,按照每个条目对应的 -log10pValue 由大到小排序的各 10 条进行条形图展示。
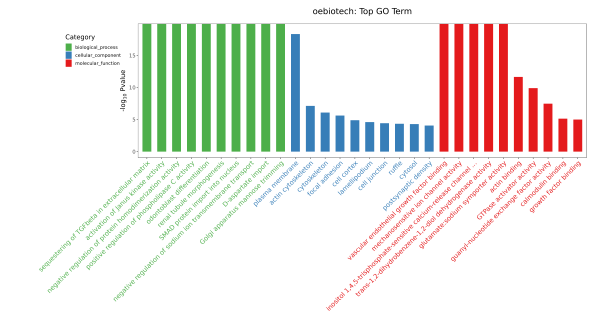
示例为自定义GO富集条形图,筛选三种分类中对应差异基因数目大于等于 5 的 GO 条目,按照每个条目对应的 ListHits 由大到小排序的各 10 条进行条形图展示,可对富集结果进行筛选。
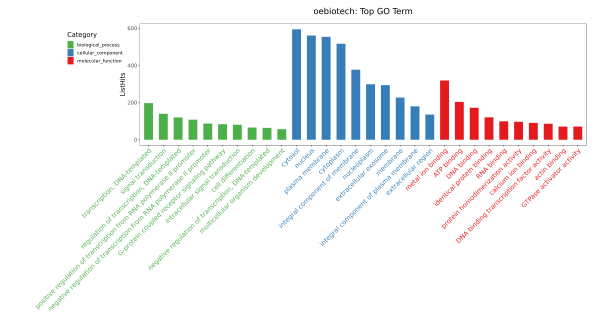
1. 输入矩阵文件(必选):
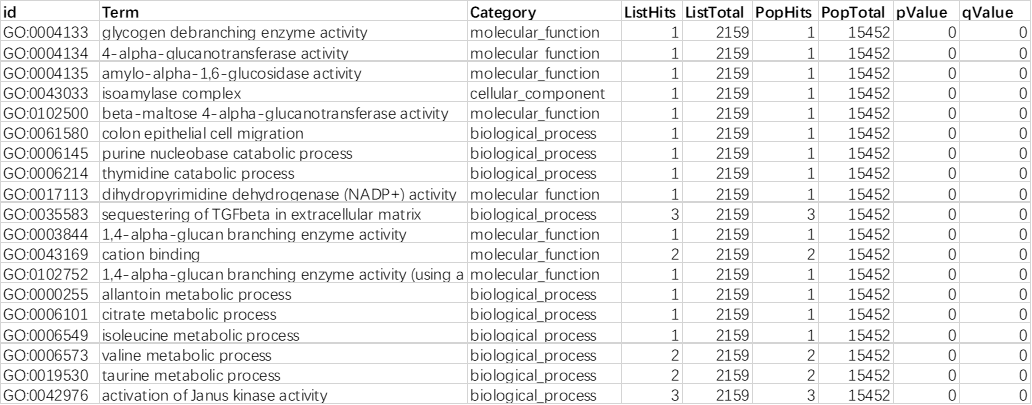
示例为OE常规转录组分析中GO富集结果,列信息需包含 "ListHits,Term,Category,pValue" ,外来数据请先调整数据格式。
蛋白代谢相关性图
通过相关性分析可以帮助衡量显著差异代谢物之间的相关密切程度,进一步了解生物状态变化过程中,代谢物之间的相互关系。相关性分析使用Pearson相关系数,Pearson积差相关系数衡量了两个定量变量之间的线性相关程度。
1.图形输出
相关性分析使用Pearson相关系数,Pearson积差相关系数衡量了两个定量变量之间的线性相关程度。红色表示正相关,蓝色表示负相关。
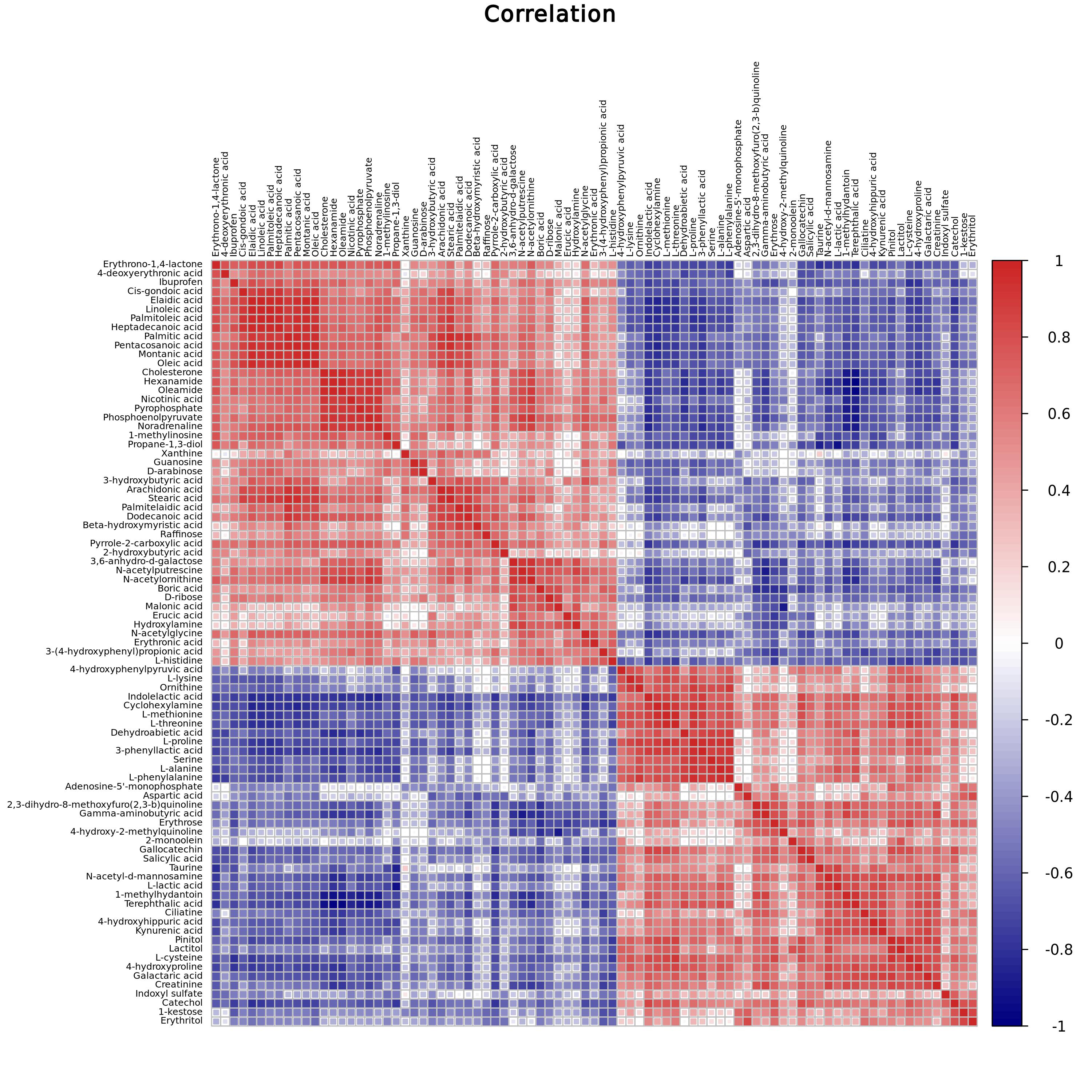
1. 表达量文件
示例数据为绘制热图所需的基因表达量矩阵文件,第一列为基因或蛋白名称,其余各列为各样品中相应基因或蛋白的表达量。

组学关联散点图
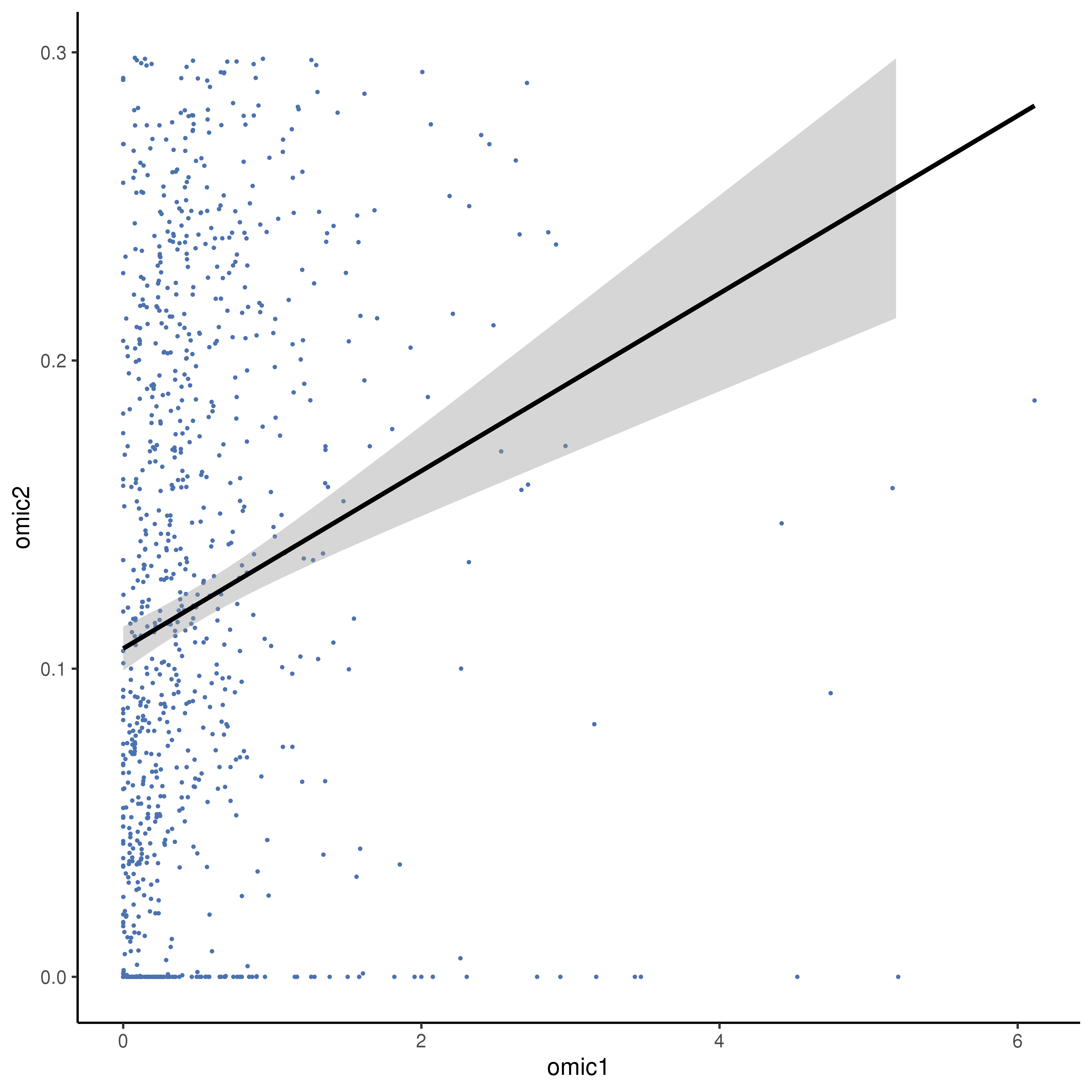
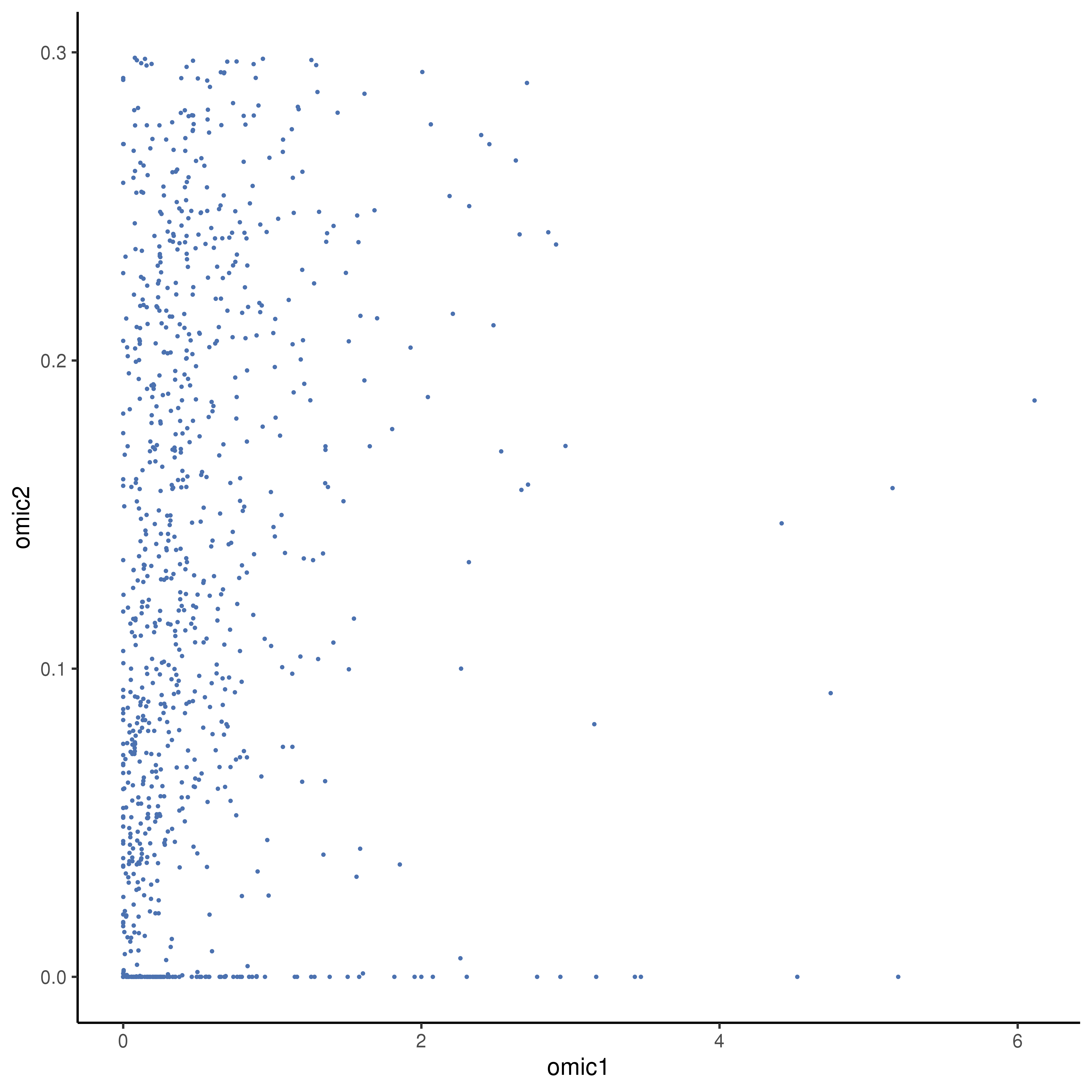
散点图(Scatter plot)可以通过两组学在二维(即水平X轴和垂直Y轴)平面分布直观表现出两者总体关系趋势。通过线性回归来衡量两组数据的相关性(可选Pearson,Spearman和 Kendall)。P值小于0.05的情况下,R2值越大,相关性越高。另外,也可以计算置信区间,用浅灰色阴影绘制在散点图中。
1.输入文件
含有3列信息,第一列对应名称(基因/蛋白/代谢物/微生物等),若包含重复,请去重。第二列表示第一个组学的表达量,第三列表示第二个组学的表达量。

1.结果说明
图中的每个点表示分别在X轴和Y轴的数值分布,通过线性回归可以来衡量两组学数据的线性关系。还可以计算两组数据的(Pearson,Spearman和 Kendall)相关性,结果保存在Scatter_plot.txt中。另外,线两边的浅灰色阴影代表置信区间。
图中的每个点表示分别在X轴和Y轴的数值分布。可以计算两组数据的(Pearson,Spearman和 Kendall)相关性,结果保存在Scatter_plot.txt中。
通过计算两组学数据的(Pearson,Spearman和 Kendall)相关性可以得到相关性系数R2和P值,P值小于0.05的情况下,R2值越大,相关性越高。
物种比例累计柱状图
柱状图是一种以矩形的长度(高度)为变量的统计图表,只包含一个变量,从形式上又可以划分为累计柱状图和躲避式柱状图等不同类型。
我们以物种在样本中所占的比例作为变量,横坐标为样本,以累计柱状图的方式展现每个样本中各物种的比例。如果提供了样本分组信息,还可以通过组内求平均的方式展现每个分组的物种比例。
1.结果示意图
该图展示了不分组情况下所有样本内的物种比例情况。横坐标为样本分析名,纵坐标为不同物种在样本中所占的比例。不同物种用不同颜色区分,下方为物种的注释信息。
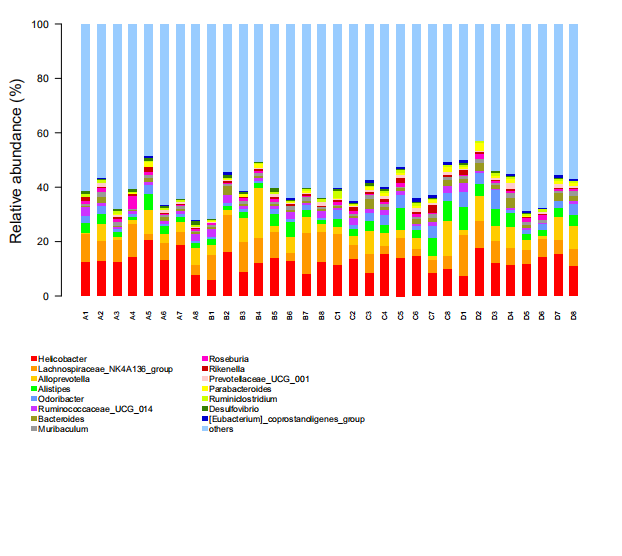
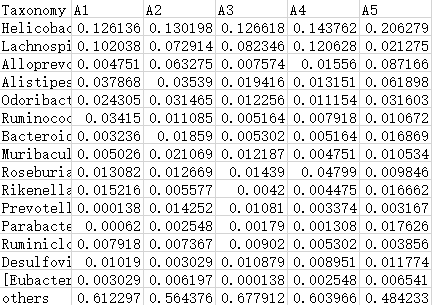
1. 物种相对丰度文件(必填)
物种相对丰度文件(tab分割文件)为必填参数。列为样本分析名,行为物种名,值为物种在样本中的相对丰度。输入文件格式支持txt和xls。
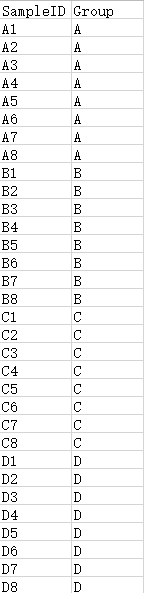
2. 样本分组信息文件(选填)
样本分组信息文件(tab分割文件)为选填参数。第一列为样本分析名,第二列为样本的分组名称。输入文件格式支持txt和xls。如果需要进行样本分组分析,则需要填此参数;如果无需进行样本分组分析,则无需填此参数。
芯片散点图
芯片数据分组比较后的差异基因数据经过quantile normalization方法归一化后绘制散点图(scatter plot),常用于评估两组数据总体分布集中趋势,图中的点代表芯片上的探针点。
1.散点图
Y轴表示实验组的表达量,X轴表示对照组的表达量,图上的每一个点表示本次结果中的基因或者探针,其中红色的点表示上调,蓝色的点表示下调,灰色的点表示没有满足差异筛选条件。上下调的倍数设置取决于分析时设置的倍数阈值。
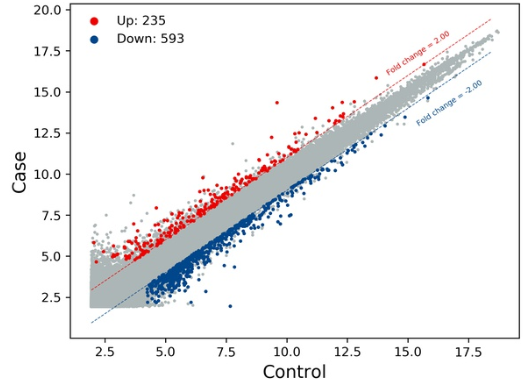
注: 结果中可以看到在上下调两倍的阈值以上,还存在着较多灰色的点,这些点满足差异倍数大于指定阈值,但是在其他差异筛选条件可能满足不了,比如差异倍数较大,但是p值也很大,这种点一般也认为是不可信的,所以标注为灰色的点。
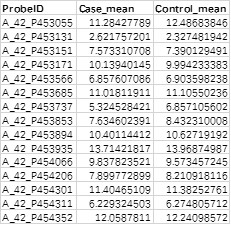
1. 所有基因或者探针的表达量检测结果
含有3列信息,第一列对应探针名称或者基因名称,若包含重复,请去重。第二列表示实验组的表达量,第三列表示对照组的表达量。
2. 差异筛选结果
含有4列信息,内容同1.1所有数据一致,额外多出一列 Regulation 表示基因或者探针的上下调情况。
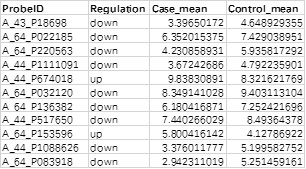
注:用于分析的数据需要进行过log2转换后的数据,芯片的分析数据一般已经进行过log2转换,若数据是测序的数据,需要将数据转换为log2(fpkm+1)后的数据才可进行展示。
微生物ROC曲线
根据特征数据丰度,如差异物种或生物标记物等,利用10折交叉验证,对每一折划分训练集及验证集,先对训练集构建随机森林模型,再用此模型预测验证集,构建ROC曲线,最后对10折进行平均处理得最终ROC曲线。
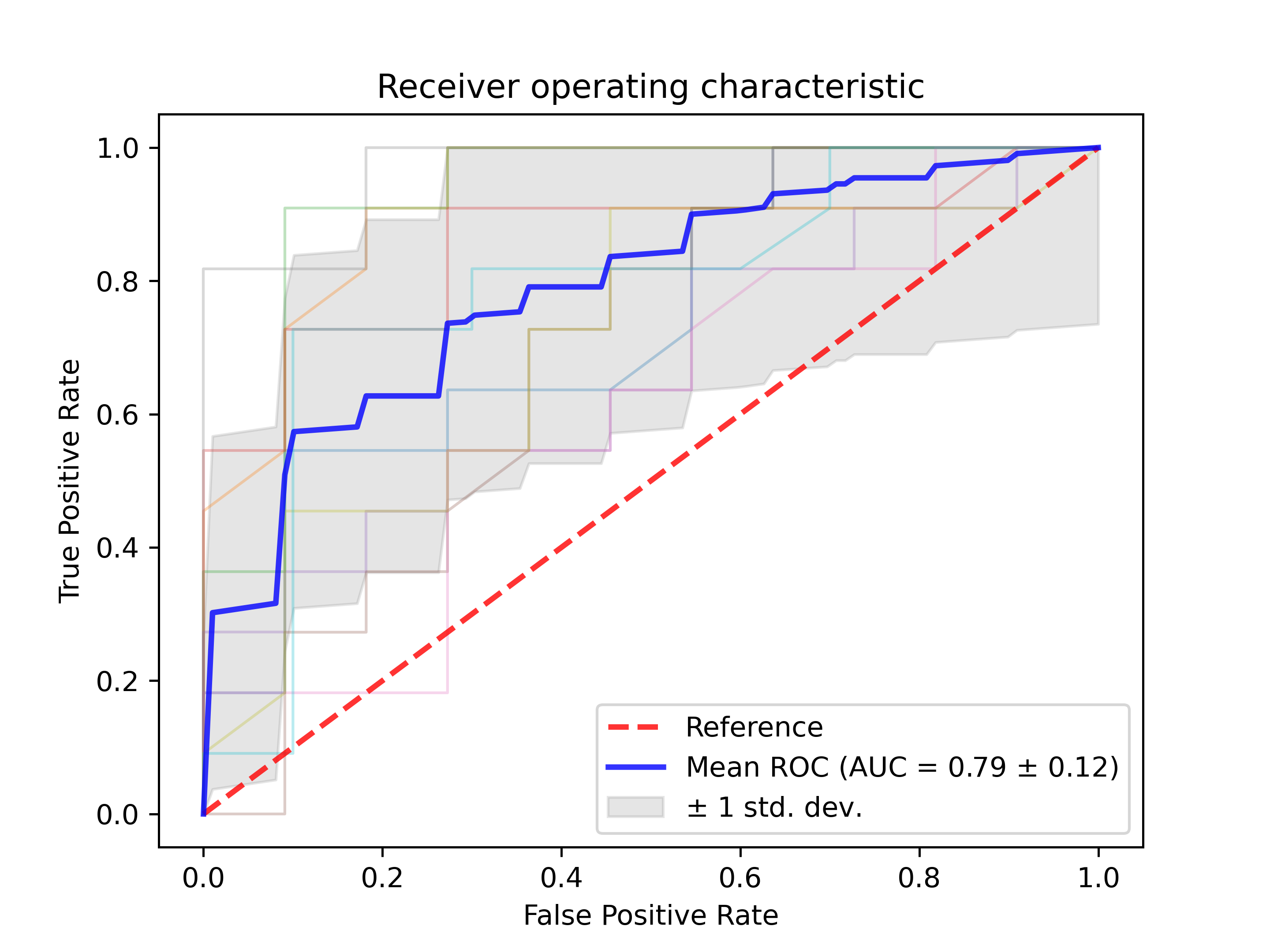
ROC曲线结果示意图
给予特征数据丰度,基于随机森林模型,利用10折交叉验证构建ROC曲线。ROC曲线横坐标为假阳性率,纵坐标为真阳性率,蓝色曲线为10折后取的平均曲线,AUC为曲线下面积,阴影部分为上下1个标准差。
1. 丰度表示例文件
物种丰度表,第一列为特征物种,表头为样品信息,其余为丰度信息。

1. 样本对应分组表示例文件
样品对应分组信息表,组数必须为2。第一列为样品名,第二列为样品对应的分组信息。

Corrplot图
corrplot 图可以用圈的大小和颜色变化来反映二维矩阵或表格中的数据信息,它可以直观地将数据值的大小以定义的圈的大小及颜色深浅表示出来。相关性 corrplot 分析通过计算物种间或环境因子与物种的相关性(Spearman 系数等),将获得的数值矩阵直观的展示到 corrplot 中。
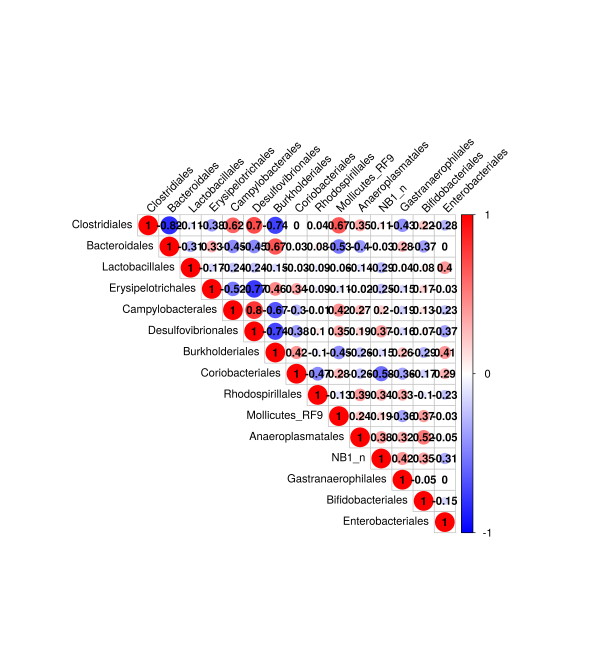
1.结果示例图
corrplot 图可以用圈的大小和颜色变化来反映二维矩阵或表格中的数据信息,它可以直观地将数据值的大小以定义的圈的大小及颜色深浅表示出来。相关性 corrplot 分析通过计算物种间或环境因子与物种的相关性(Spearman 系数等),将获得的数值矩阵直观的展示到 corrplot 中。结果图片示例文件,红色为正相关,蓝色为负相关,颜色越深、圈越大则相关性越强。
2.结果示例表
结果表格示例文件,相关系数表。

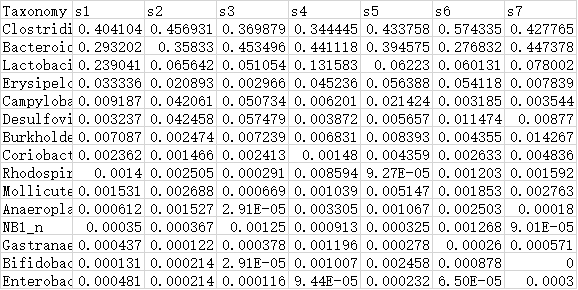
1.数据集文件
数据集文件(tab分割文件)为必填参数。内含欲计算相关性的数据,可为同一份数据,也可上传不同的两个数据集。如下面示例,列为样本分析名,行为物种名,值为物种在样本中的相对丰度。输入文件格式支持txt和xls,xlsx。
NAME
DESC
OUTPUT
DEMO1

INPUT1
DEMO2

INPUT2
DEMO3
